Lua源码阅读：基本数据类型Table

(Updated: )
源码阅读
Lua

Lua中Table数据结构的定义、初始化、查找等。

Table数据结构的定义：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
typedef union TKey {
  struct {
    TValuefields;
    int next;  /* for chaining (offset for next node) */
  } nk;
  TValue tvk;
} TKey;

typedef struct Node {
  TValue i_val;
  TKey i_key;
} Node;

typedef struct Table {
  CommonHeader;
  lu_byte flags;  /* 1<<p means tagmethod(p) is not present */
  lu_byte lsizenode;  /* log2 of size of 'node' array */
  unsigned int sizearray;  /* size of 'array' array */
  TValue *array;  /* array part */
  Node *node;
  Node *lastfree;  /* any free position is before this position */
  struct Table *metatable;
  GCObject *gclist;
} Table;
  • Table的结构中有CommonHeader成员，这是一个在lObject.h中定义的宏，包含了一些成员，所有受gc管理的对象均含有CommonHeader，其继承自GObject对象。CommonHeader 相当于来自父类的数据，在整个结构的最前面，其他成员相当于子类数据。通过这种方式可以让GCObject 指针指向所有受gc管理的lua的对象，并且CommonHeader 结构中还有当前对象的类型，可以转换成具体类型的对象。
1
2
3
4
5
/*
** Common Header for all collectable objects (in macro form, to be
** included in other objects)
*/
#define CommonHeader	GCObject *next; lu_byte tt; lu_byte marked

TValue是所有lua数据类型的集合，其包含一个类型_tt和一个value，Value类型是一个union，可以是lua的任意类型：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/*
** Tagged Values. This is the basic representation of values in Lua,
** an actual value plus a tag with its type.
*/

#define TValuefields	Value value_; int tt_

typedef struct lua_TValue TValue;

union Value {
  GCObject *gc;    /* collectable objects */
  void *p;         /* light userdata */
  int b;           /* booleans */
  lua_CFunction f; /* light C functions */
  lua_Integer i;   /* integer numbers */
  lua_Number n;    /* float numbers */
};


struct lua_TValue {
  TValuefields;
};

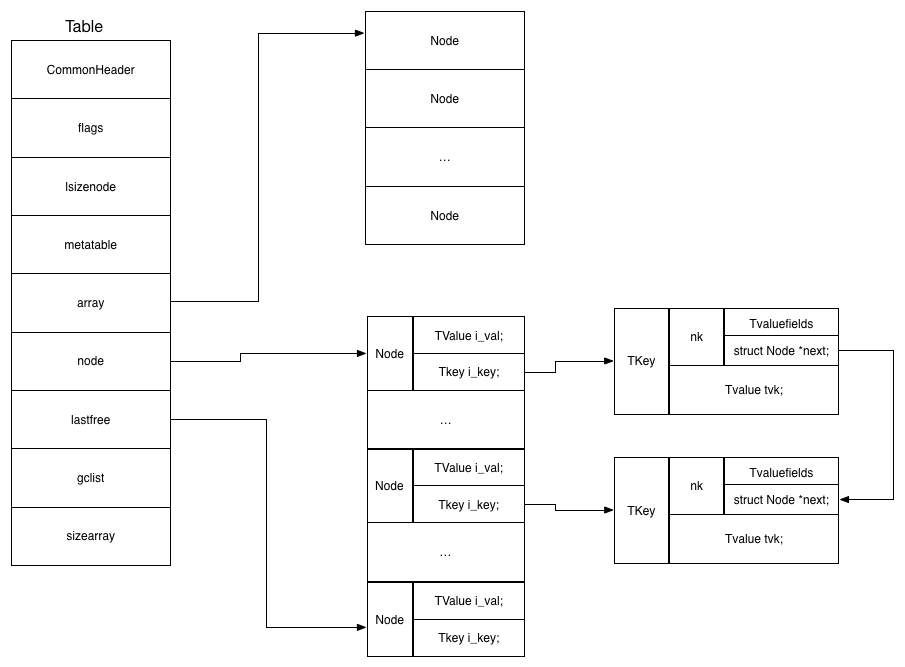
Table主要有两部分，数组和哈希：

  1. array和node是两个一维数组，array是普通的数组，成员为TValue，node是一个hash表存放key,value键值对。node的key为TKey类型，Tkey是一个union，当没有hash冲突的时候是一个TValue，当有hash冲突的时候TKey是一个struct，多一个next值，指向下一个有冲突的节点。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    typedef union TKey {
      struct {
        TValuefields;
        int next;  /* for chaining (offset for next node) */
      } nk;
      TValue tvk;
    } TKey;


    /* copy a value into a key without messing up field 'next' */
    #define setnodekey(L,key,obj) \
    	{ TKey *k_=(key); const TValue *io_=(obj); \
    	  k_->nk.value_ = io_->value_; k_->nk.tt_ = io_->tt_; \
    	  (void)L; checkliveness(G(L),io_); }


    typedef struct Node {
      TValue i_val;
      TKey i_key;
    } Node;

  2. sizearray：是数组array的大小

  3. lsizenode：2^lsizenode 的值为node 的大小

  4. lastfree：lastfree 指针的右边均由非空的或者不能访问的node (即不属于自己的空间，访问会越界)组成

  5. metatable ：元表

  6. gclist：与gc 有关，将table加入到gray表中时，gclist指向gray表中的下一个元素或者NULL

  7. flags : 这是一个byte类型的数据，用于表示这个表中提供了哪些元方法，最开始的flag为1，当查找了一次之后，如果该表中存在某个元方法，那么将该元方法对应的flag bit置为0，这样下一次查找时只需要比较这个bit就行了。每个元方法对应的bit定义在ltm.h中 。

68747470733a2f2f7261772e6769746875622e636f6d2f6c69636875616e672f4c75612d536f757263652d496e7465726e616c2f6d61737465722f7069632f7461626c652e706e67.png

Table的初始化：

1
2
3
4
5
6
7
8
9
10
Table *luaH_new (lua_State *L) {
  GCObject *o = luaC_newobj(L, LUA_TTABLE, sizeof(Table));
  Table *t = gco2t(o);
  t->metatable = NULL;
  t->flags = cast_byte(~0);
  t->array = NULL;
  t->sizearray = 0;
  setnodevector(L, t, 0);
  return t;
}

首先，为Table开辟空间，然后将其加到allgc链表上通过gc进行管理，之后初始化Table的内容。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
static void setnodevector (lua_State *L, Table *t, unsigned int size) {
  int lsize;
  if (size == 0) {  /* no elements to hash part? */
    t->node = cast(Node *, dummynode);  /* use common 'dummynode' */
    lsize = 0;
  }
  else {
    int i;
    lsize = luaO_ceillog2(size);
    if (lsize > MAXHBITS)
      luaG_runerror(L, "table overflow");
    size = twoto(lsize);
    t->node = luaM_newvector(L, size, Node);
    for (i = 0; i < (int)size; i++) {
      Node *n = gnode(t, i);
      gnext(n) = 0;
      setnilvalue(wgkey(n));
      setnilvalue(gval(n));
    }
  }
  t->lsizenode = cast_byte(lsize);
  t->lastfree = gnode(t, size);  /* all positions are free */
}

#define dummynode		(&dummynode_)

#define isdummy(n)		((n) == dummynode)

static const Node dummynode_ = {
  {NILCONSTANT},  /* value */
  {{NILCONSTANT, 0}}  /* key */
};

flag设置为全1表示没有元方法，node指向的不是NULL而是dummynode，dummynode是一个全局共享的对象（key和value均为nil），这样做可以减少NULL的判断：例如，刚初始化完table，需要查找一个key为“test”的对象，因为lsizenode为0，所以经过运算确定的位置肯定为node[0]，然后读取node[0].i_key和“test”的TKey进行比较，判断是否相同，node[0]是dummynode，所以比较结果肯定不相同，所以返回nil；如果node[0]为NULL，访问node[0]的时候必须先判断node[0]是否为NULL，否则直接访问会越界，dummynode的设计省去了NULL的判断。

Table的查找：

因为table有两部分，数组和hash表，所以查找也分为两部分来进行：

  1. 在数组中查找，如果传入的key是integer类型，而且其值-1小于sizearray的话，在数组中查找。
  2. 其他情况在hash表中查找：计算出该key的散列值，根据此散列值访问Node数组得到散列桶所在的位置，遍历该散列桶下的所有链表元素，直到找到该key为止。

在Lua中除了nil，其他类型均可以作为表的key，那么table的key是如何与其array数组与hash表的下标对应的呢？

对于array数组，如果是上述的第一种情况，则直接将key-1即得到了下标，对于hash表则需要将key转换成uint类型，然后通过计算得到下标。

通过运算将各类型转换为uint 类型的值，如将LUA_TNUMFLT 类型二进制数值转成以uint 型类 型表示，将LUA_TTABLE 的gc 指针转换为uint 类型， LUA_TSHRSTR 类型直接取其hash值，因为短字符串在构造时会计算其hash值，LUA_TLNGSTR 类型则需要通过hash函数计算其hash值。在 完成了对key 的hash运算以后，需要根据key 的hash值计算该key对应hash表中的哪个下标，计算的公式是:

1
index = hash_value & ((2^lsizenode) - 1)

其中2^lsizenode - 1 为一个二进制低位全为1 的值，和hash_value 相与可以保证hash_value超过2^lsizenode - 1 的部分为0，则得到的值一定在[0，(2^lsizenode) - 1] 区间内，此时key和hash 表的下标就对应了起来，并且不会越界。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/*
** main search function
*/
const TValue *luaH_get (Table *t, const TValue *key) {
  switch (ttype(key)) {
    case LUA_TSHRSTR: return luaH_getstr(t, tsvalue(key));
    case LUA_TNUMINT: return luaH_getint(t, ivalue(key));
    case LUA_TNIL: return luaO_nilobject;
    case LUA_TNUMFLT: {
      lua_Integer k;
      if (numisinteger(fltvalue(key), &k)) /* index is int? */
        return luaH_getint(t, k);  /* use specialized version */
      /* else go through */
    }
    default: {
      Node *n = mainposition(t, key);
      for (;;) {  /* check whether 'key' is somewhere in the chain */
        if (luaV_rawequalobj(gkey(n), key))
          return gval(n);  /* that's it */
        else {
          int nx = gnext(n);
          if (nx == 0) break;
          n += nx;
        }
      };
      return luaO_nilobject;
    }
  }
}

/*
** search function for integers
*/
const TValue *luaH_getint (Table *t, lua_Integer key) {
  /* (1 <= key && key <= t->sizearray) */
  if (l_castS2U(key - 1) < t->sizearray)
    return &t->array[key - 1];
  else {
    Node *n = hashint(t, key);
    for (;;) {  /* check whether 'key' is somewhere in the chain */
      if (ttisinteger(gkey(n)) && ivalue(gkey(n)) == key)
        return gval(n);  /* that's it */
      else {
        int nx = gnext(n);
        if (nx == 0) break;
        n += nx;
      }
    };
    return luaO_nilobject;
  }
}

Table的更新：

table 更新也分两种情况:

  1. 通过上述查找的 value 如果不是 luaO_nilobject ，直接将 value 更改即可，即table的修改和删除(将值置为nil)
  2. 查找返回的是 luaO_nilobject ，即 key 在 table 中不存在时( table 的插入操作)需要先找一个空的槽，然后完成插入操作，如果找不到空槽则需要扩容。

散列表部分的数据组织是，首先计算数据的key所在的桶数组位置，这个位置称为mainposition。相同mainposition的数据以链表形式组织：

FlowchartDiagram1.png

这部分的API包括luaH_set、luaH_setnum、luaH_setstr 这三个函数，它们的实际行为并不在其函数内部对 key 所对应的数据进行添加或者修改，而是返回根据该 key 查找到的 TValue 指针，由外部的使用者来进行实际的替换操作。

当找不到对应的 key 时，这几个 API 最终都会调用内部的 newkey 函数分配一个新的 key 来返回。

具体的更新操作如下：

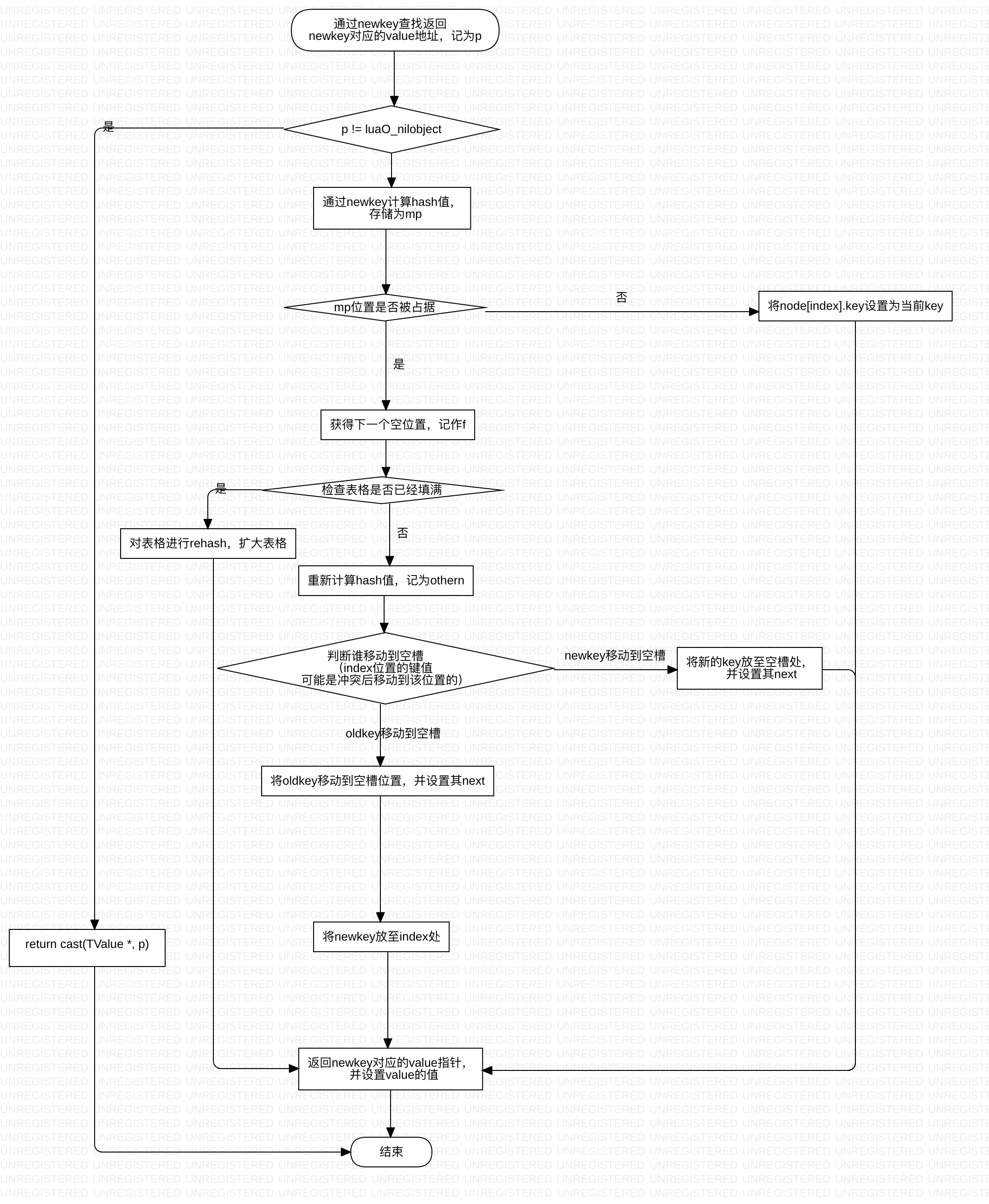
TableUpdate.png

  1. 如果查找一个空槽：

    在lua Table中有一个lastfree指针，在更新时通过该指针寻找一个空槽，lastfree 指针在最开始的时候指向NULL ，当空间不够rehash 时，lastfree 指针指向 node 数组中最后不可用的空间，如node 数组size为4 其指向的就是4 的位置(从0开始)。当需要找一个空槽时，lastfree指针向左移，判断当前位置有没有被占用，即key 是否为nil ，如果被占用则继续左移，直到找到一个空槽，或者地址大于node 的地址，即移动到了node 的前一个，表示没有找到。这种方式可以保证lastfree的右边和当前指向的位置均不可用或者被占用，可以减少在查找空槽时对非nil元素的遍历。

  2. 冲突时谁移动：

    记冲突位置为index ，找到的空槽位置为freeindex ，发生冲突位置的key 为oldkey ， 新的key 为newkey 。发生冲突时计算oldkey 的下标，如果值为index ，则将newkey 建立 到freeindex 位置处，如果oldkey 计算后不是index ，而是因为冲突被移动到index 位置的，则移动oldkey 的node到新的槽。

  3. Tkey的Next如何设置：

    lua 中的Tkey 中添加了一个next 成员，通过next 可以查找冲突位置的所有元素。比如两个元素冲突了，冲突位置为index (下标，后面的freeindex 也是下标)，这两个元素分别 为node1 、node2 ，假设将node1 移动到了另一个位置freeindex ，那么node2 则在index位置，node2 的next 为freeindex 减去index ，当需要查找node1 时，通过hash 运算找到是node2 ，比较发现不是要找的元素，此时可以通过index + next 找到freeindex 的位置，继续比较判断发现是node1 则返回结果。这种方式可以减少查找时对非冲突元素的遍 历，加快查找效率，不过也有弊端就是每个节点占用的空间会增减四个字节。

Table的扩容：

rehash操作是hash 表不可避免的，当空间不够时就需要进行扩容，而扩容后每个元素的下标就需要重新计算。对于一般的开放地址法会有一个负载因子 ，当负载因子大于某个值的时候就需要扩容，这个是为了考虑效率问题，当负载因子越来越大的时候，元素之间冲突的可能性会越来越大，导致插入和查找的时间复杂度会增大所以需要扩容降低负载因子。lua 的table没有负载因子，而是当node 的所有空间都用完的时候才会扩容(被置为nil 也算，lastfree指针不会向右移动，而判断满的条件就是lastfree 已经到了第一个元素的位置)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/*
** nums[i] = number of keys 'k' where 2^(i - 1) < k <= 2^i
*/
static void rehash (lua_State *L, Table *t, const TValue *ek) {
  unsigned int nasize, na;
  unsigned int nums[MAXABITS + 1];
  int i;
  int totaluse;
  for (i = 0; i <= MAXABITS; i++) nums[i] = 0;  /* reset counts */
  nasize = numusearray(t, nums);  /* count keys in array part */
  totaluse = nasize;  /* all those keys are integer keys */
  totaluse += numusehash(t, nums, &nasize);  /* count keys in hash part */
  /* count extra key */
  nasize += countint(ek, nums);
  totaluse++;
  /* compute new size for array part */
  na = computesizes(nums, &nasize);
  /* resize the table to new computed sizes */
  luaH_resize(L, t, nasize, totaluse - na);
}

扩容前会先统计table中的数量，将其存至nasize中；建立了一个大小为32的数组并且初始化为0，然后统计array数组中不为nil的元素个数，统计时通过分段的方式进行统计，将所有的元素按(2\^(i-1),2\^i]分段，分为32 个区间段：(0.5, 1]、(1, 2]、(2, 4]、 (4, 8] ……，统计步骤如下：

  1. 分配一个位图 nums，将其中的所有位置 0。这个位图的意义在于：nums 数组中第 i 个元素存放的是 key 在 2^(i-1)和 2^i 之间的元素数量。
  2. 遍历 Lua 表中的数组部分，计算其中的元素数量，更新对应的 nums 数组中的元素数量（numusearray函数）。
  3. 遍历 Lua 表中的散列桶部分，因为其中也可能存放了正整数，需要根据这里的正整数数量更新对应的 nums 数组元素数量（numusehash 函数）。
  4. 此时nums 数组已经拥有了当前这个 Table 中所有正整数的分配统计，逐个遍历 nums 数组，获得其范围区间内所包含的整数数量大于 50%的最大索引，作为重新散列之后的数组大小，超过这个范围的正整数，就分配到散列桶部分了（computesizes 函数）
  5. 根据上面计算得到的调整后的数组和散列桶大小调整表（resize 函数）。

调整标准：希望在调整过后，数组在每一个二次方位置容纳的元素数量都超过该范围的 50%。能达到这个目标的话，我们就认为这个数组范围发挥了最大的效率。

重新散列的代价与解决：

1
2
3
4
local a = {}
for i = 1,3 do
	a[i] = true
end
  1. 最开始，Lua 创建了一个空表
  2. 在第一次迭代中，a[1]为 true 触发了一次重新散列操作，将数组部分长度设置为 2^0，即 1，散列表部分仍为空。
  3. 在第二次迭代中，a[2]为 true 触发了一次重新散列操作，将数组部分长度设置为 2^1，即 2。
  4. 最后一次迭代中，a[3]又触发了一次重新散列操作，将数组部分长度设置为 2^2，即 4。

如果有很多很小的表要进行创建，则会对开销造成巨大的影响——可以预先填充以避免重新散列操作。

Table 的迭代：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int luaH_next (lua_State *L, Table *t, StkId key) {
  unsigned int i = findindex(L, t, key);  /* find original element */
  for (; i < t->sizearray; i++) {  /* try first array part */
    if (!ttisnil(&t->array[i])) {  /* a non-nil value? */
      setivalue(key, i + 1);
      setobj2s(L, key+1, &t->array[i]);
      return 1;
    }
  }
  for (i -= t->sizearray; cast_int(i) < sizenode(t); i++) {  /* hash part */
    if (!ttisnil(gval(gnode(t, i)))) {  /* a non-nil value? */
      setobj2s(L, key, gkey(gnode(t, i)));
      setobj2s(L, key+1, gval(gnode(t, i)));
      return 1;
    }
  }
  return 0;  /* no more elements */
}

/*
	在数组部分查找数据：
		查找成功，则返回该 key 的下一个数据
	否则在散列桶部分查找数据：
		查找成功，则返回该 key 的下一个数据
*/

一开始进入 findindex 函数，返回一个整数索引，如果这个索引在表的 sizearray 之内，则说明落入到数组部分，否则就落入到散列桶部分。

Table 取长度操作：

对Lua 中的表进行取长度的操作时，如果没有提供该表的原方法 _len，那么该操作只针对该表的序列部分进行——序列指的是该表的一个子集{1…n}，n是一个正整数，其中每个键对应的数据都不为 nil。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/*
** Try to find a boundary in table 't'. A 'boundary' is an integer index
** such that t[i] is non-nil and t[i+1] is nil (and 0 if t[1] is nil).
*/
int luaH_getn (Table *t) {
  unsigned int j = t->sizearray;
  if (j > 0 && ttisnil(&t->array[j - 1])) {
    /* there is a boundary in the array part: (binary) search for it */
    unsigned int i = 0;
    while (j - i > 1) {
      unsigned int m = (i+j)/2;
      if (ttisnil(&t->array[m - 1])) j = m;
      else i = m;
    }
    return i;
  }
  /* else must find a boundary in hash part */
  else if (isdummy(t->node))  /* hash part is empty? */
    return j;  /* that is easy... */
  else return unbound_search(t, j);
}

Table的元表：

注意事项：

  • 尽量不要在一个表中混用数组和散列桶部分，即一个表最好只存放一类数据。Lua 的实现上确实提供了两者统一表示的遍历，但这并不意味着使用者就应该混用这两种方式。
  • 尽量不要在表中存放 nil 值，这会让取长度操作的行为不稳定。
  • 尽量避免重新散列操作，因为这个操作的代价极大，通过预分配、只使用数组部分等策略规避这个 Lua 解释器背后的动作，能提升不少效率。

参考：

  • 《lua 设计与实现》codedump 著